Описание задачи:
У вас есть два конверта. В один конверт вы помещаете некоторую сумму денег, неизвестную для других и отдаёте этот конверт Али. Затем вы скрытно подбрасываете монету. Если выпадает орёл, во второй конверт вы кладёте сумму в два раза большую, чем в первом. В противном случае во второй конверт кладётся сумма в два раза меньшая. Этот конверт вы отдаёте Бабе. Али и Баба могут открыть свои конверты, не сообщая один другому суммы которые они там видят. После этого они могут (по обоюдному согласию) обменяться конвертами.
Предположим, что Али видит в своём конверте 10$. Али предполагает, что в конверте у Бабы равновероятно могут находиться 5$ или 20$. В этом случае обмен конвертами приносит Али 2,5$ (или 25 %). Аналогично Баба считает, что в конверте Али равновероятно находится сумма в два раза меньшая или большая, чем  , которая находится у него. Поэтому в среднем, при обмене конвертов, он получает
, которая находится у него. Поэтому в среднем, при обмене конвертов, он получает  . Таким образом, Баба также ожидает получить в среднем 25% дохода, по сравнению с суммой в своём конверте.
. Таким образом, Баба также ожидает получить в среднем 25% дохода, по сравнению с суммой в своём конверте.
 , которая находится у него. Поэтому в среднем, при обмене конвертов, он получает
, которая находится у него. Поэтому в среднем, при обмене конвертов, он получает  . Таким образом, Баба также ожидает получить в среднем 25% дохода, по сравнению с суммой в своём конверте.
. Таким образом, Баба также ожидает получить в среднем 25% дохода, по сравнению с суммой в своём конверте.Однако, это является парадоксальным.
Примечание: описание задачи взято с сайта Википедии: goo.gl/YvhUZ
Предварительные замечания:
Природа парадокса, как кажется, кроется либо в отождествлении ролей игроков (в случае, когда известно, что Али получает первый конверт, а Баба - второй), либо в игнорировании вероятности получить определенный конверт (когда неизвестно, кто из участников получает первый конверт). Рассмотрим оба случая.
СЛУЧАЙ 1. Али получает первый конверт, Баба получает второй:
Ожидаемая прибыль Али от обмена конвертами будет равна:
 .
.При этом ожидаемая прибыль Бабы составит:
 .
.Таким образом, Баба, как рационально действующий агент, не захочет меняться конвертами с Али.
СЛУЧАЙ 2. Участники игры не знают, кто из них получает какой конверт:
Ожидаемая прибыль каждого из участников будет равна:
 , где
, где  - вероятность получить первый конверт,
- вероятность получить первый конверт, - вероятность получить второй конверт.
- вероятность получить второй конверт.Очевидно, что:
при  прибыль участника от смены конверта равна нулю, у его противника - тоже;
прибыль участника от смены конверта равна нулю, у его противника - тоже;
 прибыль участника от смены конверта равна нулю, у его противника - тоже;
прибыль участника от смены конверта равна нулю, у его противника - тоже;при 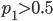 участник может получить выгоду от смены конверта, его противник получит убыток;
участник может получить выгоду от смены конверта, его противник получит убыток;
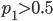 участник может получить выгоду от смены конверта, его противник получит убыток;
участник может получить выгоду от смены конверта, его противник получит убыток;при  участник оказывается в ситуации Али из Случая 1, его противник - в ситуации Бабы;
участник оказывается в ситуации Али из Случая 1, его противник - в ситуации Бабы;
 участник оказывается в ситуации Али из Случая 1, его противник - в ситуации Бабы;
участник оказывается в ситуации Али из Случая 1, его противник - в ситуации Бабы;при  участник получит убыток от смены конверта, его противник получит прибыль;
участник получит убыток от смены конверта, его противник получит прибыль;
 участник получит убыток от смены конверта, его противник получит прибыль;
участник получит убыток от смены конверта, его противник получит прибыль;при 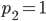 участник оказывается в ситуации Бабы из Случая 1, его противник - в ситуации Али.
участник оказывается в ситуации Бабы из Случая 1, его противник - в ситуации Али.
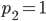 участник оказывается в ситуации Бабы из Случая 1, его противник - в ситуации Али.
участник оказывается в ситуации Бабы из Случая 1, его противник - в ситуации Али. Выводы:
Таким образом, обмен конвертами либо не приводит к росту благосостояния участников, либо не может состояться из-за нежелания одного из участников нести убытки. Отсюда, как кажется, следует, что рассматриваемого парадокса не существует в принципе.
Всё сказанное Вами вполне справедливо в отношении задачи про Али и Бабу, которая выложена в Вики под старым именем чуть больше двух недель назад. В задаче про Али-Бабу нет ни прежней симметрии конвертов (второй наполняется с помощью монеты действительно со строгими фифти/фифти), ни самого парадокса. Давайте порешаем старую задачу. Она куда более заслуживает внимания :).
ОтветитьУдалить